Les moteurs Stirling sont l'un de ces appareils qui ont fasciné de nombreux ingénieurs (y compris moi-même) au fil des ans, surtout quand nous sommes jeunes et impressionnables, avant que nous ne devenions trop cyniques à propos du monde. C'est aussi l'une de ces technologies qui n'a pas vraiment été largement adoptée, malgré les cris des YouTubers d '« énergie gratuite », donc ce n'est évidemment pas la solution parfaite pour de nombreux problèmes, mais pour certaines applications, ce sont vraiment des moteurs soignés.

L'équipe de Midé a récemment consacré de longues heures à la mise en place d'un nouveau projet Stirling pour les Marines américains. J'ai choisi le moteur à cycle Stirling pour cette application en raison de son rendement naturellement élevé et parce qu'il s'agit d'un moteur à combustion externe. Pour soutenir ce projet, j'avais une quantité importante de recherches à faire sur la théorie qui régit les moteurs Stirling - afin que nous puissions mieux concevoir une solution pour nos militaires. Dans cet article, je vais partager avec vous certaines des bases que j'ai apprises et fournir un outil pour vous aider à visualiser le cycle de Stirling. Espérons que cet outil vous aidera à revérifier certains des calculs de base que vous aimeriez faire, ainsi qu'à fournir un moyen pratique de tracer certaines des propriétés pour un cycle de Stirling idéal.

Figure 1 : Un premier prototype de moteur Stirling fabriqué à Midé dans le cadre d'un projet pour le Corps des Marines.

Aperçu

Un moteur Stirling est une saveur spécifique de moteur thermique formulée par Robert Stirling en 1816; cela signifie qu'il peut transformer le flux de chaleur en travail mécanique (comme faire tourner un vilebrequin). Le terme clé est «flux de chaleur»; il faut qu'il y ait deux "réservoirs" séparés, et ces réservoirs doivent être à des températures différentes pour que cet écoulement se fasse entre eux. Si vous placez un conducteur thermique entre les deux réservoirs au fil du temps, ils approcheront tous les deux de la même température, indiquant que l'énergie « circule » du réservoir chaud vers le réservoir froid.

Le moteur Stirling exploite ce flux d'énergie du chaud au froid et en siphonne une partie sous forme de travail mécanique. Le moteur Stirling a besoin d'une section chaude et d'une section froide isolées l'une de l'autre, la façon intelligente dont un fluide de travail est acheminé entre les deux sections permet au moteur de produire un travail mécanique. La chaleur est transférée de la section chaude au moteur, une partie de l'énergie quitte le moteur sous forme de travail mécanique utile et une partie est transférée sous forme de transfert de chaleur vers la section froide. N'oubliez pas que l'énergie ne peut jamais être détruite, donc si vous additionnez toute l'énergie quittant le moteur (c'est-à-dire le travail utile + le transfert de chaleur dans la section froide), elle doit être égale à la quantité d'énergie entrant dans le moteur sous forme de transfert de chaleur depuis la section chaude. Ce bilan énergétique est la première loi de la thermodynamique et tient toujours.

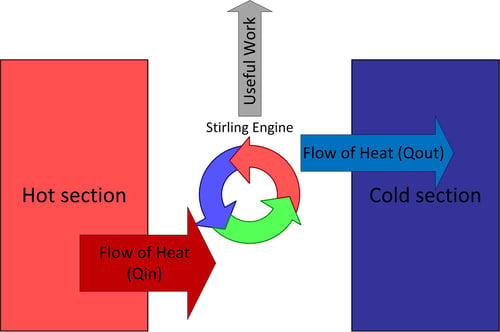
Figure 2 : Diagramme thermodynamique du moteur thermique

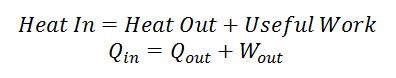
Équation 1 : Première loi de la thermodynamique pour un moteur Stirling, la première loi est simplement un bilan énergétique du système

Commentaires sur l'efficacité thermique

Le rapport entre le travail utile et le transfert de chaleur dans le moteur est appelé efficacité thermique. Considérez-le comme le rapport de ce que vous voulez (travail mécanique utile) divisé par les coûts (transfert de chaleur dans le moteur).

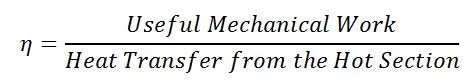
Équation 2 : Calcul de l'efficacité thermique d'un Stirling

L'efficacité ne peut jamais être supérieure à 1. Une efficacité de 1 signifierait que tout le transfert de chaleur dans le moteur devient un travail utile et qu'il n'y a aucun transfert de chaleur vers la section froide. Une efficacité de 0 indique qu'aucun travail utile n'est produit et que tout transfert de chaleur de la section chaude quitte simplement le moteur sous forme de transfert de chaleur vers la section froide. Si vous mettiez deux briques l'une à côté de l'autre, une chaude et une froide, dans une boîte parfaitement isolée et que vous les laissiez là pendant un certain temps, vous reviendriez pour trouver deux briques chaudes. Il s'agit techniquement d'un moteur thermique avec un rendement de 0 ; la chaleur a été transférée de la brique chaude à la brique froide avec un rapport de 1: 1, ne produisant aucun travail utile dans le processus.

Il s'avère que l'efficacité ne peut jamais non plus être égale à 1 ; désolé pour ça, la deuxième loi de la thermodynamique est un vrai fluage. Déduire la relation qui limite les niveaux d'efficacité physiquement possibles est un tout autre sujet, mais cela s'appelle l'efficacité de Carnot, du nom de Nicolas Léonard Sadi Carnot. Il a pu postuler l'efficacité maximale à laquelle on pouvait s'attendre sans violer la deuxième loi de la thermodynamique. On peut calculer le rendement Carnot en ne connaissant que les températures de la partie chaude et de la partie froide entre lesquelles travaille un moteur thermique donné. Cela signifie que vous n'aurez jamais un moteur thermique qui ne rejette pas au moins une partie de la chaleur vers la section froide.

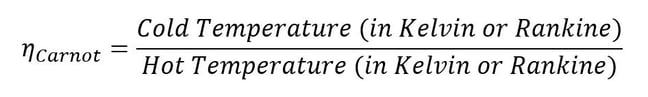
Équation 3 : L'efficacité Carnot limite les performances réalistes du moteur

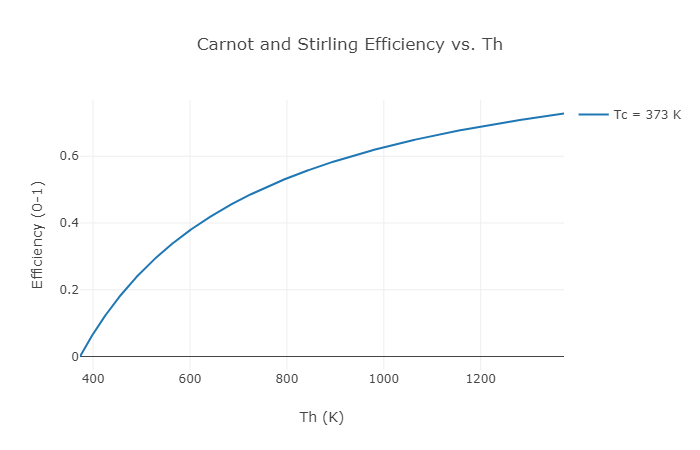
Figure 3 : Exemple d'efficacité thermique Carnot ou Stirling par rapport à la température de la section chaude

Lorsque l'on trace l'efficacité Carnot possible compte tenu de la température de la section chaude, on peut voir que plus la différence de température entre le côté chaud et le côté froid est grande, plus l'efficacité possible est élevée. Tous les moteurs ne peuvent même pas théoriquement (pour ne pas dire de manière réaliste) atteindre l'efficacité Carnot. Par exemple, le moteur diesel parfait ne pourrait jamais, même dans un monde parfait, égaler l'efficacité du moteur thermique Carnot théorique. Certains autres types de moteurs thermiques peuvent égaler le moteur Carnot en performances théoriques. Le moteur Stirling en est un exemple. Par conséquent, l'efficacité de Carnot à une température donnée de section chaude et de section froide est égale à l'efficacité de Stirling entre les mêmes sections chaude et froide.

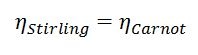
Équation 4 : L'efficacité thermique idéale de Stirling est égale à l'efficacité de Carnot

Pour faire fonctionner un Stirling en continu, vous devez avoir une section chaude qui est constamment chauffée par une source et une section froide qui est refroidie d'une manière ou d'une autre. Sans chauffer constamment la section chaude et refroidir la section froide, suffisamment de chaleur serait finalement transférée entre les deux pour que vous vous retrouviez avec deux sections chaudes. Une fois que cela se produit, vous n'avez plus ce différentiel de température entre les sections, l'efficacité chuterait à 0 et aucune chaleur ne serait transférée à travers le moteur puisqu'il n'existe aucun différentiel de température.

Pour le moteur de Midé, la partie chaude est chauffée en brûlant des matériaux de biomasse, et la partie froide est refroidie par de l'eau qui traverse ensuite un radiateur. Cela nous permet de maintenir la section chaude à environ 900 K et la section froide à environ la température de l'eau bouillante (373 K). Si vous faites le calcul pour calculer l'efficacité de Carnot (et donc l'efficacité de Stirling), ces températures signifient qu'on ne pourrait jamais s'attendre à obtenir plus d'une efficacité de 0,58 sans que l'univers n'implose. Malheureusement, tout de suite, presque la moitié de l'énergie que vous mettez dans notre moteur est GARANTIE de sortir sous forme de transfert de chaleur perdue vers la section froide. En ce moment, nous ne parlons que de moteurs absolument parfaits, et c'est tout ce qui sera discuté dans ce post, mais dans le monde réel, il y a toutes sortes d'autres facteurs qui rendent impossible d'atteindre le niveau d'efficacité Carnot. Tu es une superstar si tu peux avoir la moitié de Carnot.

Le moteur Stirling en tant que cycle

Les moteurs thermiques sont cycliques, et c'est le cas du moteur Stirling. Dans le cas d'un moteur alternatif, comme celui que nous avons construit, un processus se produit entre la section de maintien et la section froide, qui se répète à une certaine fréquence. La chaleur est absorbée dans le moteur par impulsions, puis rejetée dans la section froide et sous forme de travail par impulsions. Habituellement, un volant d'inertie est ajouté au moteur pour lisser ces impulsions et faire tourner le mécanisme. La chaleur de la section chaude est transférée à la section froide via un type de fluide de travail (air, hélium, hydrogène, azote ou tout autre type de gaz, certains sont meilleurs que d'autres). Pour un Stirling, il est possible de décrire le cycle thermodynamique en quatre sections.

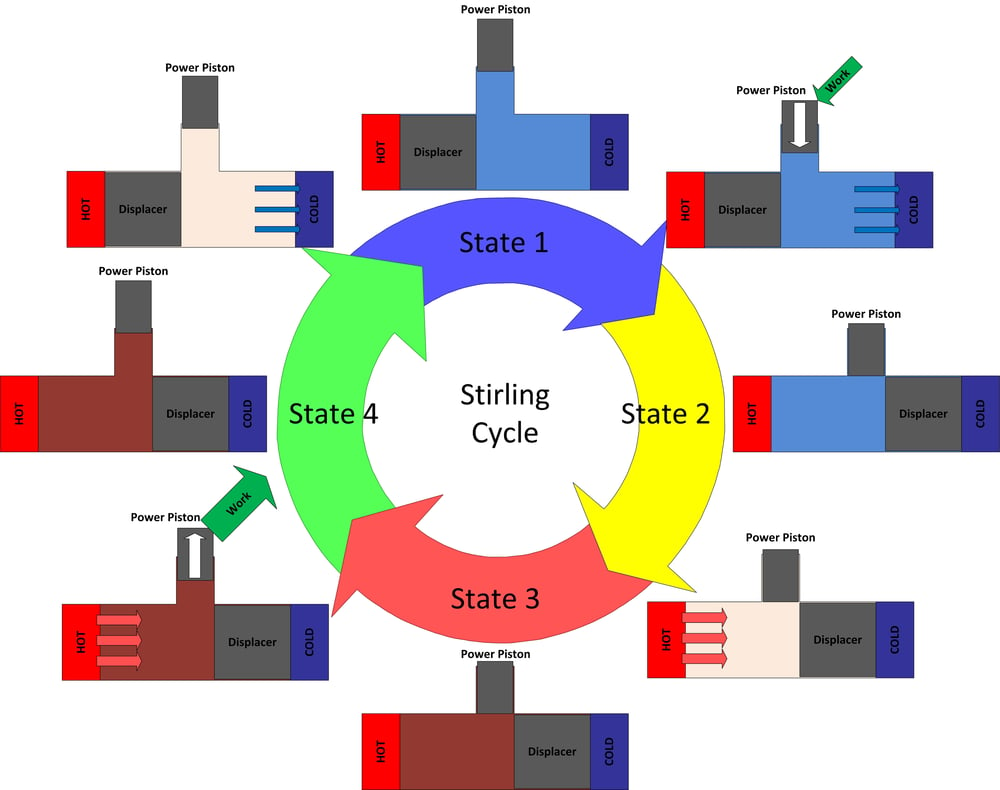
Figure 4 : Le cycle de Stirling idéal

État 1 à 2

À l'état 1, le fluide de travail est à un volume maximum, une température minimum et une pression minimum. De l'état 1 à l'état 2, le piston de puissance comprime le fluide de travail tandis que la chaleur est transférée hors du système qui maintient le fluide de travail à une basse température constante. Lorsque le moteur est dans l'état 2, le fluide de travail est dans un état comprimé (haute pression et faible volume), mais reste à la même température que l'état 1. Le travail nécessaire pour comprimer le volume est fourni par l'énergie stockée dans le moteur. volant.

État 2 à 3

À l'état 2, le fluide de travail est à un volume minimum, une température minimum et une pression moyenne. Entre les états 2 et 3, le volume est maintenu constant tandis que la chaleur est ajoutée par la section chaude pour augmenter la température.

État 3 à 4

À l'état 3, le fluide de travail a atteint une température maximale, une pression maximale, tout en étant également à un volume minimal. De l'état 3 à 4, le fluide de travail est autorisé à se dilater, effectuant un travail utile pendant qu'il le fait. Pendant le processus d'expansion, plus de chaleur est ajoutée pour maintenir le système à une température constante. L'énergie fournie lors de cette expansion l'emporte sur l'énergie qui était nécessaire pour comprimer le volume entre les états 1 et 2, fournissant un travail net positif.

État 4 à 1

Pour ramener le moteur à l'état 1 où il a commencé, la chaleur est retirée du fluide de travail tandis que le volume est maintenu constant.

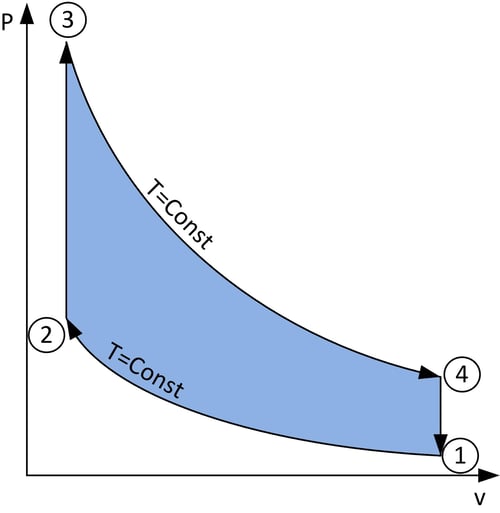
Figure 5 : Une boucle montrant la relation entre la pression et le volume pendant un cycle du moteur Stirling, et avec chaque état étiqueté

Résumé des équations

Il est possible de calculer les propriétés du fluide à tous ces différents états avec les formules suivantes :

De plus, le travail utile produit peut être calculé avec la formule suivante. CR signifie "Compression Ratio" (volume maximal du moteur divisé par le volume minimal du moteur). Veuillez noter que cette formule donne la quantité de travail par unité de masse de fluide de travail par révolution du moteur Stirling. Les températures doivent également être dans une échelle absolue (c'est-à-dire Rankine ou Kelvin).

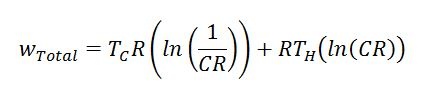
Équation 5 : Travail par unité de masse de fluide de travail fourni par un moteur Stirling idéal par tour (cycle)

Il est important de garder à l'esprit que tous ces chiffres présentés concernent le cycle de Stirling idéal, qui n'existera jamais dans la vie réelle, tous les vrais moteurs sont des approximations des cycles thermodynamiques idéaux. Savoir modifier ces relations idéales pour refléter le monde réel est un tout autre sujet, qui pourrait être traité dans un prochain article !

Configurations Stirling réelles

Afin de contrôler le moment où la chaleur est transférée vers ou depuis le fluide de travail, la plupart des moteurs Stirling ont ce qu'on appelle un piston "plongeur" ​​qui empêche simplement le contact entre le fluide de travail et la section chaude ou la section froide en fonction de sa position. Pour modifier le volume du système, il existe généralement un type de piston de puissance qui va et vient dans un alésage de cylindre, souvent ce piston est relié à un vilebrequin afin de collecter le travail utile.

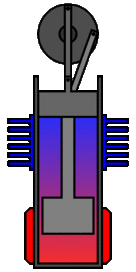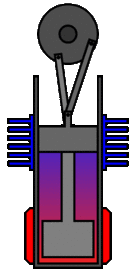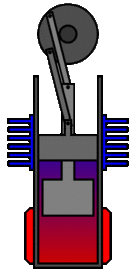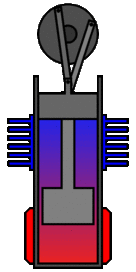
Un ingénieur peut choisir de plusieurs façons de lier mécaniquement le piston de puissance, le piston de déplacement et les échangeurs de chaleur afin de produire les effets nécessaires pendant un cycle de Stirling. Aucun mécanisme n'imite parfaitement les mouvements nécessaires, donc dans les vrais moteurs Stirling, une source de perte est "l'approximation" du cycle qui est nécessaire pour construire une vraie machine. Deux des types de configurations de moteur les plus courants sont le type bêta et le type alpha. Le moteur Midé Stirling est du type bêta.

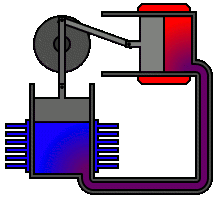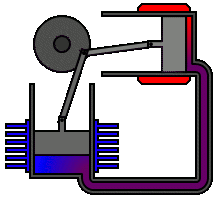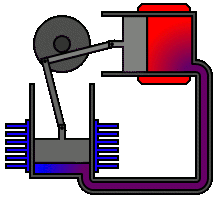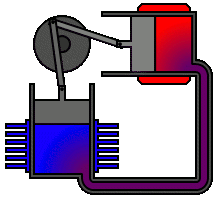
Figure 6 : Un vrai moteur Stirling, configuration alpha